Applied Orbital Dynamics Pt. 1: The Sputnik Paradox
- The Italianmoose

- May 5, 2020
- 5 min read
On the 4th of October 1957 scientists and engineers of the Soviet Union made history by launching the first artificial satellite. Sputnik 1 was a shiny silver beach-ball of a satellite with four whip antennas for its transmitter. It contained enough batteries to last for two weeks of transmission after it separated from its launcher (a predecessor to the legendary Soyuz). This being space, it lasted for three. Always pack more than you'll need.

Sputnik was launched into a very low orbit, at its lowest a mere 215 km from the Earth's surface. The generally assumed line where "space" begins is at 100 km. There isn't a hard line in reality, the atmosphere just goes on getting thinner and thinner. So there's still a small but not insignificant amount of drag. Sputnik's orbital velocity was around 8 kilometers per second, which is not slow by any means! Even hitting very little at that speed has quite an impact over time. So after three months Sputnik had re-entered Earth's atmosphere proper, in the correct manner as a ball of flame.
Prior to its demise, as its orbit became lower and lower, something happened which to the lay person is not intuitive: Sputnik got faster. In normal life the force of drag acts to slow an object to a stop, however in space the interaction results in a different result. The key is the concept of energy. For our purposes, energy comes in a number of forms. The forms we care about here are kinetic (from motion) and gravitiational potential (from gravity). These two are familiar to anyone who has thrown a ball in the air. The throw gives it some kinetic energy, which is then transferred into gravitational potential energy as the ball rises. This transfer occurs at a very predictable rate.
Now, let's do something weird. Throw the ball sideways. For a heavy, small ball we can ignore (the posh word is "neglect", or "consider negligible") the air in the way of the ball. It will fall to the ground. Nothing world shattering there. What if we threw it faster? In the immortal words of Douglas Adams, "throw yourself at the ground and miss".
In fact Sir Isaac Newton came up with a thought experiment (i.e. imagined) firing a cannonball so fast that it would continue to be pulled towards the Earth and miss. To work out how things would be affected by gravity and to solve the motion of celestial bodies from first principles he sat down to develop calculus, the mathematics of change, therefore cementing his reputation with schoolchildren across the globe. Gottfried Leibniz developed a system of calculus at the same time (debate raged over who was first), and developed most of the way calculus is actually written today.
Prior to Newton and Leibnitz the astronomer Tycho Brahe had painstakingly collected data about the motions of the planets in the sky. His assistant Johannes Kepler then developed his "Laws of Planetary Motion" based upon these measurements. So Kepler knew these laws worked based upon data, but didn't have an underlying theory. Later it was realised that solutions of Newton's law of gravitation for two bodies match Kepler's equations. However this is only the case when you have one small body moving around one much larger one. For example a satellite moving closely around the Earth. In more complex systems, for example a satellite somewhere between the Earth and the Moon, the solution is far more complex - the 3 Body Problem. For many purposes, only slight corrections to Kepler's laws work great.
So, back to Sputnik, and some slightly scary maths. All this thinking, arguing, calculus, etc. gets us to a very simple [1] equation of the speed of an object as it moves around a much larger one:
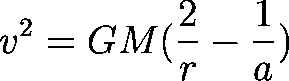
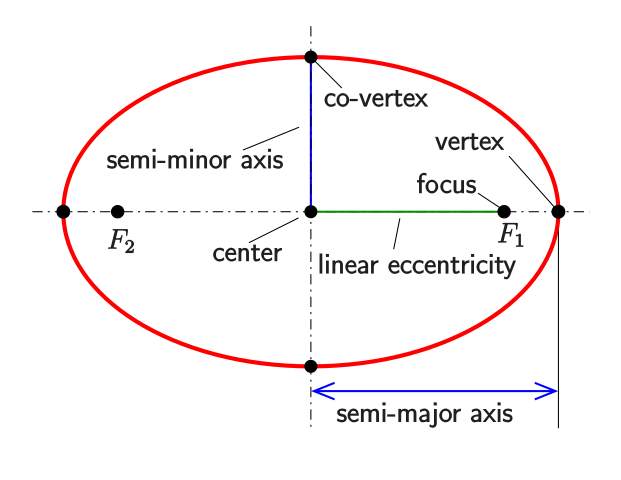
The big G is the graviational constant. This is a constant value which is essentially the exchange rate between the mass of two objects divided by the square of the distance between them, and the force they exert on each other. It cannot be derived, and must be measured. This has been done to a fine degree, where the uncertainty is measured in a few tens of parts per million. The big M is the mass of the larger body. Mass is a measure of how much "stuff" makes up the object, and is measured in kilograms. This is different to weight, which is a measure of how much force is exerted upon the object by gravity, and is in Newtons (yeah, he gets a unit of measurement named after him too). The combination of G and M is often known more precisely than either of the two separately, because it can be derived from astronomical observations which are very, very precise. However to separate the two you need to know G from laboratory experiments, and the level to which you are unsure of the value of G can be more than you are uncertain of your measurement of G and M together. The little "r" is your distance from the center of the massive object, as this model treats all objects as points in space. The little "a" is related to the total amount of energy the orbit has, which also corresponds to half the long axis of the ellipse shape most orbits move around - the "semi-major-axis", see below [2]. The point (called a vertex) closest to the object you're orbiting (called the focus) is called the "periapsis", and the furthest the "apoapsis". Around different bodies they have different specific names. For example the Earth has perigee and apogee; the Sun has perihelion and apohelion.
Now, if we introduce some atmospheric drag to this, what will happen? Drag removes energy from an object, and transfers it to kinetic energy in the atmosphere. This is also known as heat! As the object smacks into atmospheric atoms it transfers energy to them. With enough atoms this reduction in kinetic energy becomes apparent to the object. The heating to the atmosphere in general is negligible. So our semi-major axis is reduced. With an elliptical orbit, where your distance from the object you're orbiting changes, you will be spending some time in thicker atmosphere and some time in thinner atmosphere. Thicker and thinner here are very relative terms here. At this altitude the atmosphere is millions of times thinner than at sea level. Having most of the drag force concentrated at one end of your orbit means that the other end of your orbit is the one most affected. If we're throwing our ball, if we throw it less hard it will not reach as high a height but it still starts at our hand. This means we will (at this point) be slower as we pass through the lowest point in the orbit. Feels natural. In fact, I have a neat graph!
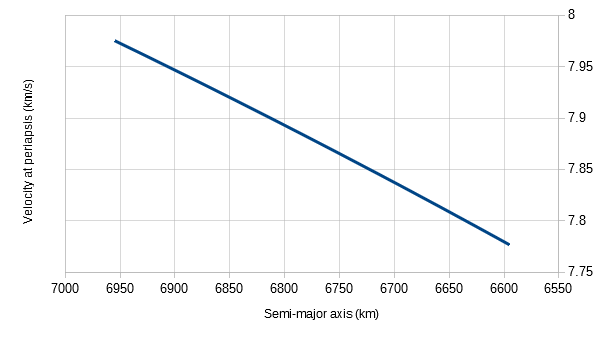
So, as we lose energy and move along the graph, if we're keeping the periapsis radius the same, we slow down. Now, if we reach a point where the semi-major axis has reduced to be equal to the periapsis, which means the orbit is a circle rather than an ellipse, the atmospheric density is more or less the same all the way around the orbit. Thus the drag is similar all around the orbit. So the satellite spirals downwards, which we can approximate as a set of circular orbits decreasing in size. Mathmatically, a circular orbit is where "r" is the same as "a" in the equation above. Now, as we spiral in towards our inevitable doom, what happens to our speed?
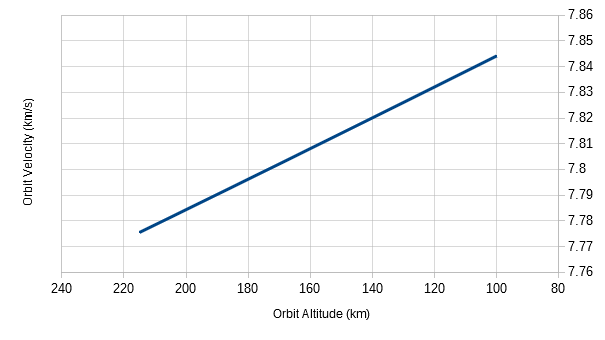
Well that's weird. Now we speed up as we spiral down. Mathmatically it makes perfect sense, but to an first-time observer this seems very strange. The object would appear to slow down over time, and then speed up again. This is the Sputnik paradox!
[1] - It could be so much worse, trust me. I'm just happy with an equation that doesn't need a computer to solve.
[2] - Yes, if you want to be pedantic it's moving in a straight line through curved space. Thanks Einstein.
Did you enjoy this? I always appreciate pizza: https://www.buymeacoffee.com/italianmoose







Comments